SLM-MUX: Orchestrating Small Language Models for Reasoning

With the rapid development of language models, the number of small language models (SLMs) has grown significantly. Although they do not achieve state-of-the-art accuracy, they are more efficient and often excel at specific tasks. This raises a natural question: can multiple SLMs be orchestrated into a system where each contributes effectively, achieving higher accuracy than any individual model? Existing orchestration methods have primarily targeted frontier models (e.g., GPT-4) and perform suboptimally when applied to SLMs. To address this gap, we propose a three-stage approach for orchestrating SLMs. First, we introduce SLM-MUX, a multi-model architecture that effectively coordinates multiple SLMs. Building on this, we develop two optimization strategies: (i) a model selection search that identifies the most complementary SLMs from a given pool, and (ii) test-time scaling tailored to SLM-MUX. Our approach delivers strong results: Compared to existing orchestration methods, our approach achieves up to 13.4% improvement on MATH, 8.8% on GPQA, and 7.0% on GSM8K. With just two SLMs, SLM-MUX outperforms Qwen 2.5 72B on GPQA and GSM8K, and matches its performance on MATH. We further provide theoretical analyses to substantiate the advantages of our method. In summary, we demonstrate that SLMs can be effectively orchestrated into more accurate and efficient systems through the proposed approach.

Takeaway 1: Orchestrating Small Language Models Outperforms a Single Large Model

A key question motivating our work is whether multiple small language models (SLMs), when effectively orchestrated, can match or exceed the performance of a single large language model (LLM). To investigate this, we compare our SLM-MUX system—built using just two SLMs—against Qwen 2.5 72B, a state-of-the-art large model with approximately 72 billion parameters. We evaluate both systems on three challenging reasoning benchmarks: MATH, GPQA, and GSM8K.

Results. As shown in Table 1, our SLM-MUX achieves remarkable results. Using only two carefully selected SLMs (Mistral Small 24B and Qwen2.5 7B), SLM-MUX significantly outperforms Qwen 2.5 72B on GPQA (49.9% vs. 44.9%, a gain of +5.0%) and GSM8K (93.7% vs. 90.4%, a gain of +3.3%). On MATH, SLM-MUX achieves 81.9% accuracy, nearly matching the 82.3% of Qwen 2.5 72B. These results demonstrate that properly orchestrated SLMs can rival or surpass models nearly 10× larger in parameter count.

Analysis. This performance advantage stems from two key factors. First, different SLMs exhibit complementary strengths: one model may excel at algebra while another performs better on geometry. By selecting outputs based on confidence scores, SLM-MUX leverages these complementary capabilities effectively. Second, our approach avoids the pitfalls of discussion-based methods (which harm SLM performance, as shown in Takeaway 2) by using a confidence-based selection mechanism that amplifies strengths rather than errors. This demonstrates that the path forward may involve orchestrating multiple smaller, specialized models rather than continuously scaling single models to ever-larger sizes.

Benchmark	SLM-MUX (2 SLMs)	Qwen 2.5 72B (Single LLM)	Δ (Gain)
MATH	81.9 ± 0.2%	82.3 ± 0.5%	-0.4%
GPQA	49.9 ± 1.8%	44.9 ± 0.5%	+5.0%
GSM8K	93.7 ± 0.2%	90.4 ± 0.3%	+3.3%

Takeaway 2: Discussion-Based Orchestration Harms SLM Performance

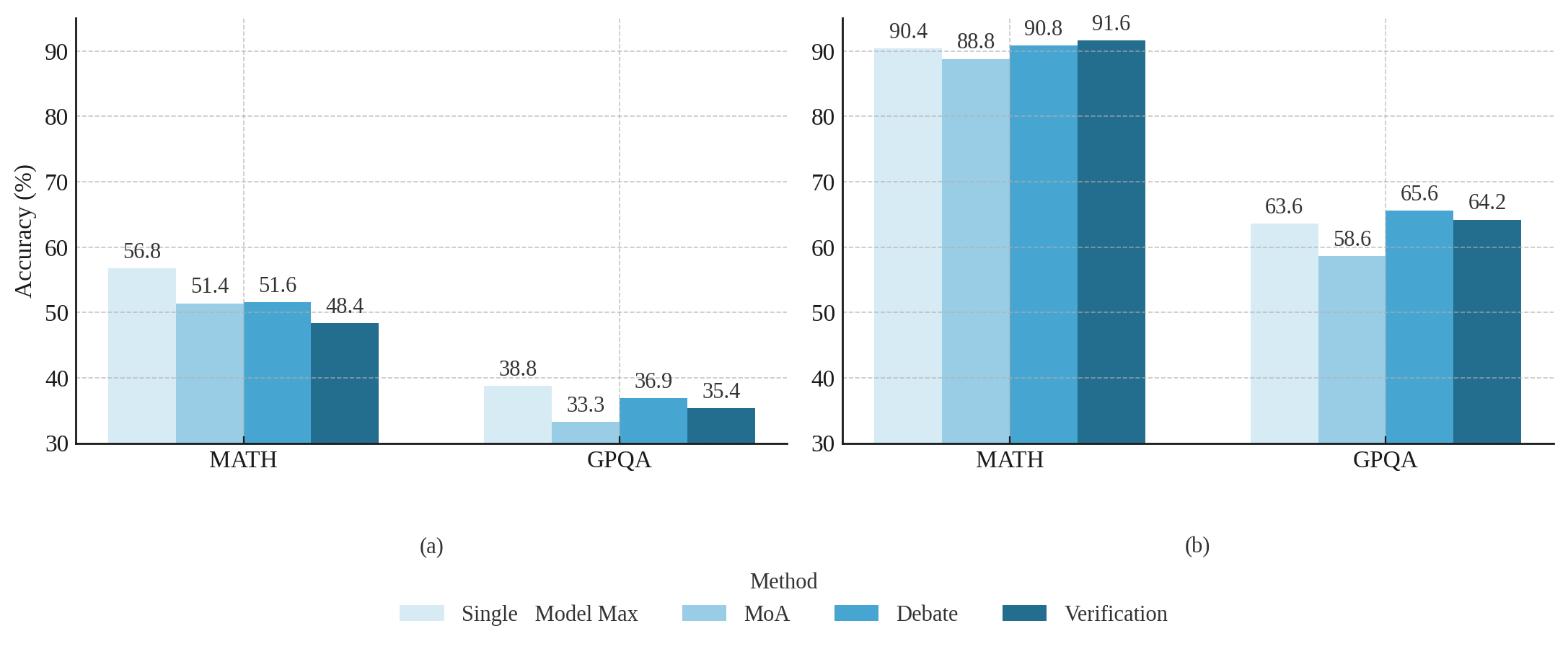
A natural question arises: if existing orchestration methods work well for frontier LLMs like GPT-4 and DeepSeek V3, shouldn't they also work for SLMs? To test this assumption, we conducted a systematic comparison of three prominent discussion-based approaches—LLM-Debate, Mixture-of-Agents, and Multi-Agent Verification. We ran these methods on two different model groups: (1) frontier LLMs (DeepSeek V3, Gemini 2.0 Flash, GPT-4o) and (2) SLMs (Llama 3.1 8B, Mistral 8×7B, Gemma 2 27B), using identical experimental settings and evaluation on MATH and GPQA benchmarks.

Results. The results reveal a striking divergence. While discussion-based methods successfully improve frontier LLM accuracy (up to 2% gains), the same methods consistently fail when applied to SLMs. Not only do they fail to surpass the best individual SLM in the group, but they can actually harm performance— reducing accuracy by up to 5.5% in some cases. This counterintuitive finding challenges the assumption that orchestration strategies transfer seamlessly across model scales.

Analysis. Why do these methods fail for SLMs? Our investigation reveals that SLMs exhibit a problematic form of "groupthink" during discussions. Instead of critically evaluating and correcting each other's mistakes, smaller models tend to reinforce incorrect reasoning patterns, amplifying errors rather than mitigating them. This suggests that the collaborative deliberation mechanisms that work for large models— which have stronger reasoning and self-correction abilities—break down when models lack sufficient capability to distinguish correct from incorrect reasoning. The appendix provides detailed empirical examples illustrating this phenomenon.

Takeaway 3: SLM-MUX Achieves SLM Orchestration Where Existing Methods Fail

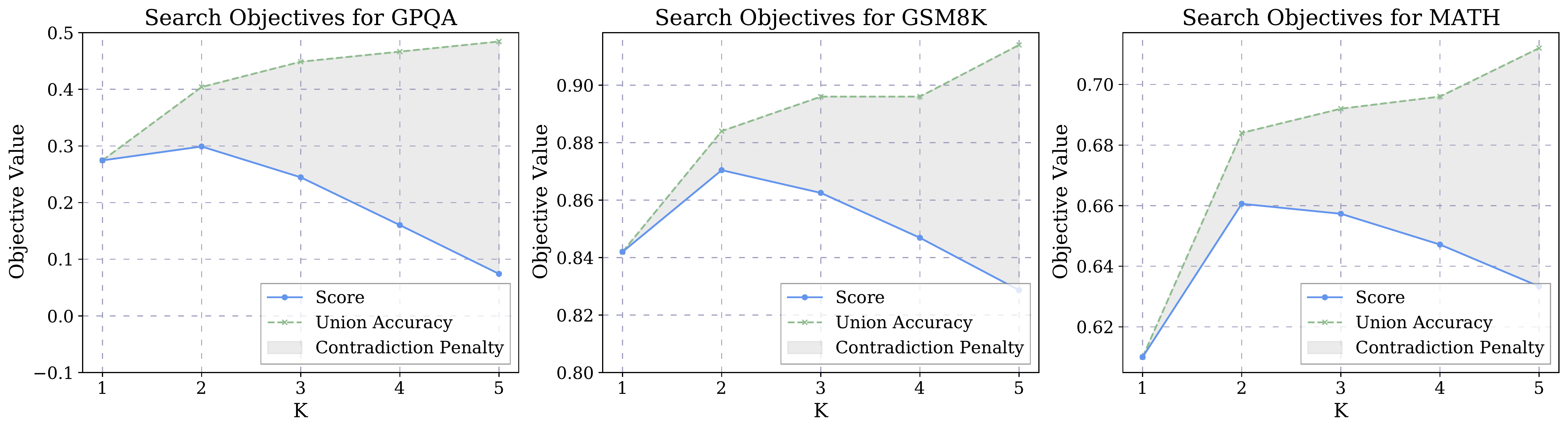
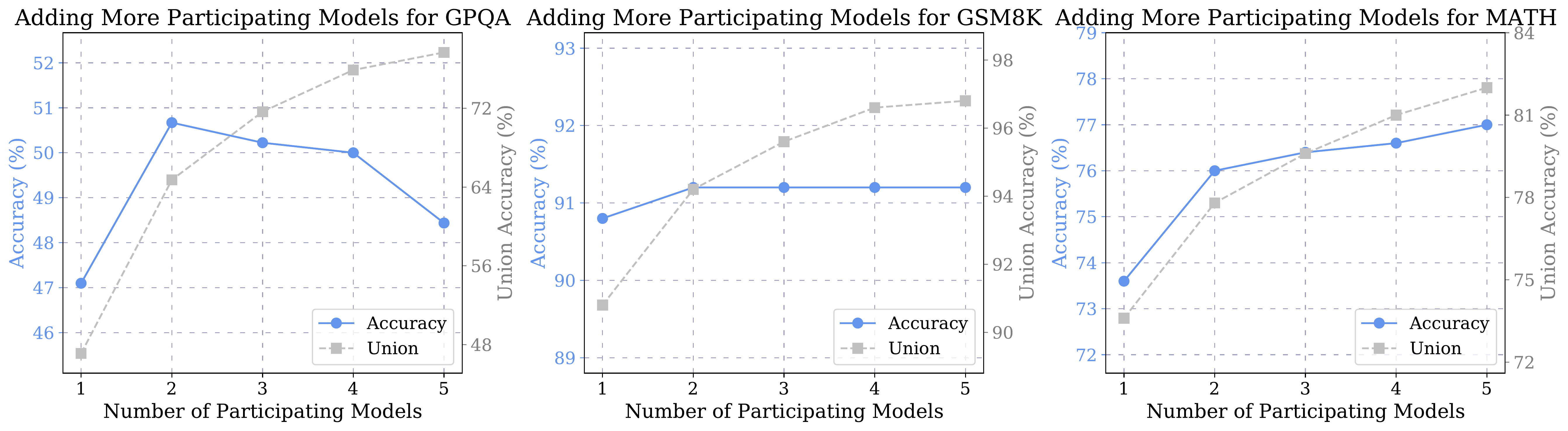
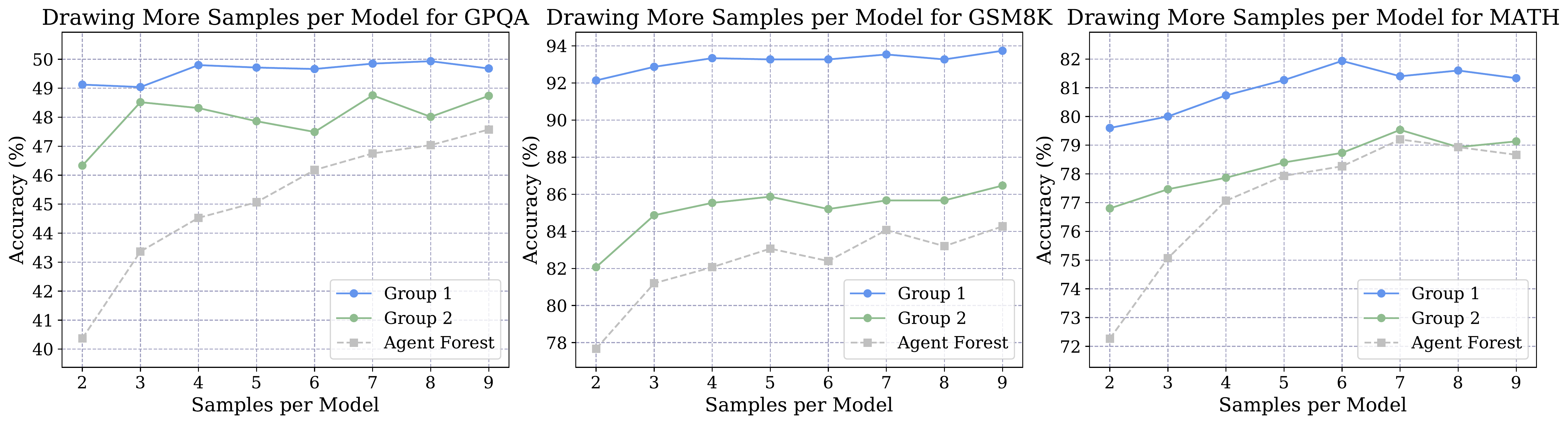
Having demonstrated that discussion-based orchestration methods fail for SLMs (Takeaway 2), a natural question arises: can SLMs be orchestrated successfully at all? To answer this, we evaluate our proposed SLM-MUX against the same baselines that failed in Takeaway 2. We use the same experimental setup with three SLMs (Mistral 8×7B, LLaMA 3.1 8B, and Gemma 2 27B) and test on MATH, GPQA, and GSM8K benchmarks.

Results. Unlike existing orchestration methods that fail to outperform individual models when applied to SLMs, SLM-MUX consistently achieves substantial accuracy gains. Compared with other orchestration approaches, our method yields up to 13.4% improvement on MATH, up to 8.8% on GPQA, and up to 7.0% on GSM8K. These results demonstrate that SLM-MUX successfully orchestrates SLMs where existing methods fail, providing a clear architectural advantage over alternative orchestration approaches.

Analysis. The key to SLM-MUX's success lies in its confidence-based selection mechanism. Rather than forcing models to discuss and potentially amplify errors (as in discussion-based methods), SLM-MUX allows each model to independently generate multiple responses and estimates confidence by counting answer frequency. The system then selects outputs from the most confident model, effectively leveraging the complementary strengths of different SLMs. As shown in our output attribution analysis, SLM-MUX successfully draws upon diverse models to produce final answers, demonstrating that it effectively exploits the heterogeneity that exists across SLMs—something that discussion-based methods fail to achieve.

Method	MATH Acc (%)	GPQA Acc (%)	GSM8K Acc (%)
Mixture-of-Agents	51.4 ± 2.2	33.3 ± 3.4	81.6 ± 1.7
LLM-Debate	51.6 ± 2.2	36.8 ± 3.4	80.8 ± 1.8
Multi-Agent Verification	48.4 ± 2.2	35.3 ± 3.4	86.4 ± 1.5
SLM-MUX (Ours)	61.8 ± 1.2	42.1 ± 0.3	87.8 ± 0.6
Single-Best	56.8 ± 2.2	38.9 ± 3.5	84.2 ± 1.6
Single-Best-SC	58.0 ± 2.2	42.4 ± 3.5	86.8 ± 1.5

Takeaway 4: Model Selection Search Boosts SLM-MUX Performance

A natural question arises: which models should be orchestrated together? Not all combinations are equally effective—if one model is weaker across all dimensions, it provides no benefit when paired with a stronger one. In contrast, combining models with complementary strengths (e.g., one excelling in algebra, another in geometry) allows the system to succeed where a single model would fail. To address this, we develop a model selection search strategy that systematically evaluates and identifies model subsets with complementary strengths.

We construct a validation set of 500 questions sampled from the training splits of MATH, GPQA, and GSM8K. Our candidate pool consists of five SLMs: Gemma 2 27B, Llama 3.1 8B, Mistral Small 24B, Mixtral 8×7B, and Qwen2.5 7B. The search procedure considers orchestrations with K=2 to 5 models and is guided by an objective function that balances union accuracy (percentage of questions solvable by at least one model) while penalizing contradictions (when models provide conflicting answers).

Results. Table 3 shows the top-performing two-model combinations identified by our search for each benchmark, along with their evaluation on the held-out test set. Across benchmarks, these optimized orchestrations yield consistent improvements over the strongest individual models: accuracy increases by 4.5% on MATH, 4.4% on GPQA, and 4.3% on GSM8K. This contrasts with Takeaway 3, where naive three-model combinations provide little to no benefit on GPQA, demonstrating that proper model selection is crucial for effective orchestration.

Analysis. Figure 3 illustrates the underlying trade-off in model selection. While union accuracy rises with additional models (grey line), the contradiction penalty also grows (grey shaded area). The overall objective score (blue line) captures this balance. On GPQA and GSM8K, performance peaks early and then declines or plateaus despite increasing union accuracy, because adding more models increases the frequency of contradictory predictions. When models disagree, SLM-MUX must select one output based on confidence scores—and incorrect selections become more likely as contradictions grow. This reveals that effective orchestration requires finding the optimal balance rather than simply maximizing the number of models.

Benchmark	Group	Model Selection	Best Single (Acc. %)	Composed (Acc. %)	Δ (Gain)
MATH	1	Mistral Small 24B Qwen2.5 7B	75.5 ± 1.5	80.0 ± 0.7	+4.5
	2	Qwen2.5 7B Llama 3.1 8B	75.5 ± 1.5	77.7 ± 0.7	+2.2
GPQA	1	Gemma 2 27B Mistral Small 24B	45.1 ± 2.8	49.5 ± 1.8	+4.4
	2	Llama 3.1 8B Mistral Small 24B	45.1 ± 2.8	48.8 ± 0.8	+3.6
GSM8K	1	Mistral Small 24B Qwen2.5 7B	88.5 ± 0.7	92.8 ± 0.6	+4.3
	2	Llama 3.1 8B Mixtral 8×7B	80.8 ± 2.1	85.2 ± 0.7	+4.4

Takeaway 5: Test-Time Scaling Impacts SLM-MUX in Different Ways

Beyond the basic SLM-MUX architecture, we investigate two complementary strategies for scaling computational resources at test time: (1) Adding More Participating Model Types—increasing the number of distinct SLMs in the orchestration from 2 to 5 models, and (2) Drawing More Samples per Model—generating multiple independent responses from each model and using them to improve confidence estimation. These two dimensions offer different trade-offs between accuracy and computational cost.

Adding More Participating Model Types

We evaluate how performance changes as we increase the number of models in the orchestration. For each ensemble size (K=2 to 5), we apply our model selection search to identify the optimal combination, then evaluate SLM-MUX on the validation set.

Results. The effect of adding more models varies substantially across benchmarks (Figure 4a). On GPQA, accuracy peaks at K=2 models and declines thereafter. On GSM8K, performance quickly saturates at two models with no further gains. In contrast, on MATH, accuracy continues to improve as additional models are included. Interestingly, despite these divergent trends in final accuracy, the union accuracy (the percentage of questions solved by at least one model) consistently increases with more models across all benchmarks.

Analysis. This divergence reveals a fundamental tension: while adding models expands the set of questions that can be answered (higher union accuracy), it also increases the frequency of contradictory predictions among models. When models disagree, SLM-MUX must select one output based on confidence scores—and incorrect selections become more likely as contradictions grow. This explains why GPQA and GSM8K show declining or plateauing performance despite growing union accuracy. The optimal number of models depends on the specific benchmark and the degree of complementarity among available SLMs.

Drawing More Samples per Model

We examine the second scaling dimension by varying the number of samples drawn from each model (from 2 to 9 samples) while keeping the model set fixed. We compare SLM-MUX against Agent Forest, a competitive baseline method, using identical model configurations to ensure fair comparison.

Results. Drawing more samples per model yields consistent improvements across all three benchmarks (Figure 4b). Unlike the model-count scaling dimension, this strategy shows no signs of diminishing returns within the tested range. Moreover, SLM-MUX systematically outperforms Agent Forest across all sample budgets, with the largest margin observed on GPQA (+5.9% at 2 samples), where individual model accuracy is lowest. At higher sample counts, SLM-MUX maintains its advantage (+1.2% on GPQA, +2.2% on GSM8K, +0.3% on MATH when using the best sample count for each method).

Analysis. Increasing samples per model provides more reliable confidence estimates, allowing SLM-MUX to make better output selections. This explains the consistent gains across benchmarks. The larger improvements on GPQA suggest that sample scaling is particularly valuable when base model performance is weaker, as additional samples help distinguish between truly confident correct answers and overconfident incorrect ones. This scaling dimension offers a more predictable path to accuracy improvements compared to adding more model types.